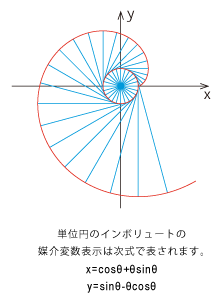糸巻きに巻いてある糸をピンと張ったままほどいていくとき、糸の先端が描く軌跡がインボリュートとなります。子供の頃、糸巻きで遊んだことを思い出しますが、それも空間的認識作業であると共に、数学的感覚とも連動していたわけです。

左の式で媒介変数と言われても、今ではよくわかりませんが、糸がほどけていく軌跡をたどっていくという行為から連想させられる数々の事柄が、数学的式という単純な文字列になっていることを知ると、もしかしてすべての行為が式で表現できるのではないかと思うこともあります。

また、インボリュートは歯車の曲線にも使用されています。インボリュートを使うと、なめらかに隙間なく歯車がかみ合うそうです。糸巻きと歯車……2つのもののまったく唐突な出会いにイメージの飛躍をさせられ、曲面の魅力を倍増させられます。

しかし考えてみると、なめらかな回転運動というイメージが、2つのものを結びつけているように思います。何気なく見ていた歯車が、インボリュートによりできていたことを知ると、歯車を見る目も変わってきます。隙間なくなめらかに動く歯車の謎が、少しわかったような気がします。

糸がほどけていく軌跡としてのインボリュートにイメージを重ね合わせ、デザインしました。

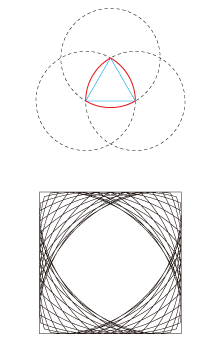正三角形の頂点を中心として、一辺を半径とする円弧を描いてできる図形がルーローの三角形です。

この図形を見ていると、どうしても幅が狭いところと広いところがあるように思いますが、実は等幅という特異な性質があります。つまり、マンホールのフタが円でできているため、決して落ちることがないようにルーローの三角形でフタを造っても、円と同様に決して落ちることはありません。どこを測っても等幅なわけです。

また、このルーローの三角形はなんと、ロータリーエンジンに応用されていたのです。子供の頃、なぜあんな形のエンジンが成り立つのかと不思議に思ったものですが、このような形状特性があったからなのでした。

さらに、左下の図のようにルーローの三角形を回転していくと、正方形になります。この特性を利用すれば、ドリルの刃をルーローの三角形にすれば、四角の穴をあけることができるわけです。木材に四角の穴があいていれば、ノミで削り出したか、このルーローの三角形の刃のドリルで穴をあけているはずです。

正三角形だけではなく、正五角形などその他の正多角形でも成り立ちます。

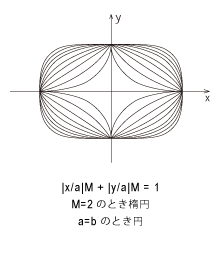楕円の中のスーパー楕円と思いきや、実は逆で、スーパー楕円の中の一つの特殊な場合（M＝2のとき）に楕円となります。式を比べてみれば当然で、スーパー楕円の式には指数Mがあるので、曲線の形が大きく変形していきます。円柱を斜めに切ったものが楕円であり、長方形の角に丸みをつけていったものがスーパー楕円という、曲線の生成経緯を見れば質の違う曲線というのが納得できるでしょう。

スーパー楕円は広場のロータリー形状や、テーブル、ホットプレート、建築物、スーパーエッグなど、幅広く利用されている馴染みの深い曲線です。これらのものに使用されているスーパー楕円は指数2分の5で、四角でもなく丸すぎずといった、絶妙なバランスの美しい曲線であるため広く利用されています。

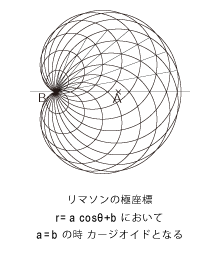左図は、点Aが中心で点Bを通る円の円周上の点と、点Bを直径とする円の包絡線が、カージオイド曲線になるという性質を利用して描いた図です。円の包絡線によって浮かび上がる外形の「ハートマーク」がカージオイド曲線＝心臓形です。

カージオイドはリマソンの一種です。リマソンの数式を極座標で表すと〈ｒ＝a cosθ+b〉になります。この数式で〈a＝b〉のとき、カージオイド（心臓形）となるのです。

アンテナの指向特性のグラフを見ると、きれいなハート形＝カージオイドになっています。この波形を読むことにより、その電波がどの方角からきているのか（＝指向性）がわかるそうです。

円の包絡線とはおもしろいものです。左の図を見ると、平面図ではなく立体図に見えてきます。果たして、3Dの場合どういった空間になるのでしょうか、そして数式はどうなるのでしょうか。

2Dの空間の、単純な円の包絡線が数式で表されるカージオイドとなり、完成した図が立体へと浮かび上がり、3D投影図へと変わる――。数学の世界は想像力をかきたててくれます。

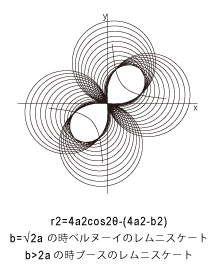左図は、直角双曲線上に中心を持ち、かつ原点を通る円の包絡線がレムニスケート曲線になるという性質を利用して描いた図です。円の包絡線によって浮かび上がる中央の「∞」マークがレムニスケート曲線です。

いくつかの単純な数式で描かれる図形の組み合わせにより、このような美しい「かたち」が現れます。「∞」マークのレムニスケート自体の数式は複雑で「かたち」を想像することはできませんが、左図のように作図の結果、いつの間にか浮かび上がった図形が特別な曲線であるということを知るとき、幾何学の不思議さとおもしろさを感じさせられます。

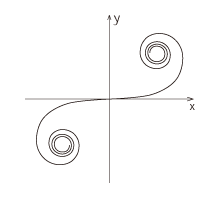曲率が道のりに比例するので、道路の曲線に利用されます。車の速度を一定にして、同じ早さでハンドルを切ってみましょう。道のカーブに沿って車が進むはず？

ループ式のジェットコースターを見てみましょう。横から見てみると真円とはなっていないことに気づくはずです。初めてのループコースター（1895年米国コニーアイランド）は真円で造られたのですが、直線からカーブにかかったときの衝撃（＝G）が大きく、「むちうち」になる人が出てきてしまいました。そこで、この曲線「クロソイド」が利用されたのです。クロソイド曲線を利用することにより、カーブにかかるときのGを低減し安全性を高めることができるとともに、楕円状となる軌道がスリルを増幅し、おもしろさを増すこともできたのです。

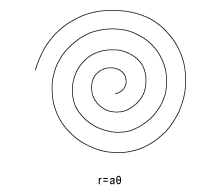代数螺旋の一種。いわゆる渦巻きのイメージ。揚水装置にも応用される、親しみのある螺旋。ドリ－ムキャストでおなじみ。

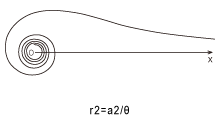代数螺旋の一種。数式からは想像もつかない美しい曲線。